Aptitude Important Notes & Short Tricks on Height & Distance

Important Notes & Short Tricks on Height & Distance

Today we will be covering a very important topic from the Advance Maths part of the Quantitative Aptitude section that is – Important Notes & Short Tricks on Height & Distance. 

Short Tricks on Height & Distance

Angle of Elevation: Let AB be a tower/pillar/shell/minar/pole etc.) standing at any point C on the level ground is viewing at A.

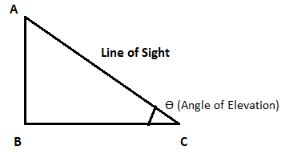
The angle ,which the line AC makes with the horizontal line BC is called angle of elevation .so angle ACB is angle of elevation.

Angle of Depression: If observer is at Q and is viewing an object R on the ground ,then angle between PQ and QR is the angle of depression .so angle PQR is angle of depression.

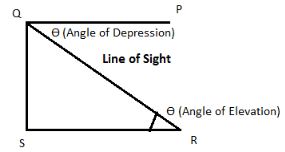
Numerically angle of elevation is equal to the angle of depression.

Both the angles are measured with the horizontal.

Previous year Questions based on Height & Distance asked in SSC CGL Exam and SSC CGL Tier II Exam.

1. The thread of a kite is 120 m long and it is making 30° angular elevation with the ground .What is the height of the kite?

Solution:

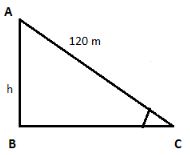
Sin 30° = h/120

1/2 = h/120

h = 60m

2. A tree bent by the wind .The top of the tree meets the ground at an angle of 60°.If the distance between the top of the foot be 8 m then what was the height of the tree?

Solution:

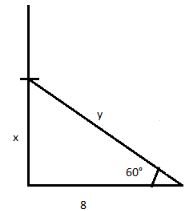
tan 60° = x/8

√3 = x/8

x = 8 √3

y cos 60° = 8/y

1/2 = 8/y

y = 16

therefore height of the tree = x+y

= 8√3+16

= 8(√3+2)

3. The angle of elevation of the top of a tower from a point on the ground is 30° . On walking 100m towards the tower the angle of elevation changes to 60° . Find the height of the tower.

Solution:

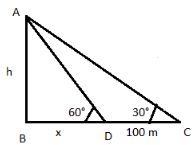
In right triangle ABD,

tan 60° = h/x

√3 x = h

x = h/√3

Again , in right triangle ABC ,

tan 30 = h/x+100

1/√3 = h/x+100

√3 h = x+100

√3 h = h/√3 + 100

√3 h – h/√3 =100

3 h - h/√3    =100

2 h = 100√3

h = 50√3

By short trick:

d = h (cot Ɵ1 - cot Ɵ2)

h = 100/(√3-1/√3) = 100*√3/2 = 50√3

Ɵ1 = small angle

Ɵ2 = large angle

d = distance between two places

h = height

4. From the top of a temple near a river the angles of depression of both the banks of river are 45° & 30°. If the height of the temple is 100 m then find out the width of the river.

Solution:

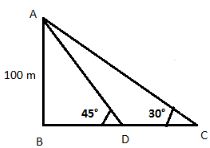
tan 45° = AB/BD

1 = 100/BD

BD = 100

tan 30 ° = AB/BC

1/√3 = 100/BC

BC = 100 √3

Width of the river , CD = BC - BD = 100 (√3-1)

When height of tower is 1 m then width of river is √3-1

Since height of tower is 100 m

Therefore ,

Width of river is 100(√3-1)m

By short trick:

Same formula can be used in this question too i.e.

d= h (cot Ɵ1 - cot Ɵ2)

5. The angle of elevation of the top of a tower from a point is 30 °. On walking 40 m towards the tower the angle changes to 45°.Find the height of the tower?

Solution:

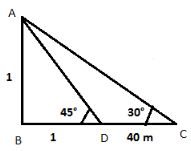
tan 45° = AB/BD

1 = AB/1

Therefore AB = 1

tan 30° = AB/BC =>1/√3 = 1/BC

therefore BC= √3

Now CD =√3-1 m and height of tower is 1 m

1 m = 1/√3-1

Therefore 40 m  = 1/√3-1.40 = 40/√3-1

= 20 (√3+1)m

By trick:

40 = h(√3-1)

H  = 40/(√3-1) = 20 (√3+1)m