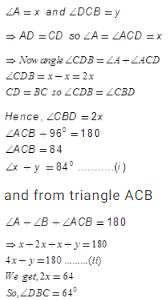Aptitude Important Notes & Concepts on HCF & LCM

Important Notes & Concepts on HCF & LCM

Important Notes on HCF & LCM

HCF & LCM are acronym for words, Highest common factor and Lowest common multiple respectively.

1. H. C. F

While we all know what a multiplication is like 2 * 3 = 6. HCF is just the reverse of multiplication which is known as Factorization. Now factorization is breaking a composite number into its prime factors. Like 6 = 2 * 3, where 6 is a composite number and 2 & 3 are prime number.

“In mathematics, the Highest Common Factor (HCF) of two or more integers is the largest positive integer that divides the numbers without a remainder. For example, the HCF of 8 and 12 is 4.”

Calculation

- By Prime Factorizations

Highest Common Factor can be calculated by first determining the prime factors of the two numbers and then comparing those factors, to take out the common factors.

As in the following example: HCF (18, 42), we find the prime factors of 18 = 2 * 3 * 3 and 42 = 7 * 2 * 3 and notice the "common" of the two expressions is 2 * 3; So HCF (18, 42) = 6.

- By Division Method

In this method first divide a higher number by smaller number.

• Put the higher number in place of dividend and smaller number in place of divisor.
• Divide and get the remainder then use this remainder as divisor and earlier divisor as dividend.
• Do this until you get a zero remainder. The last divisor is the HCF.
• If there are more than two numbers then we continue this process as we divide the third lowest number by the last divisor obtained in the above steps.

First find H.C.F. of 72 and 126

72|126|1

72       

54| 72|1

              54

              18| 54| 3

                    54

                      0 

H.C.F. of 72 and 126 = 18

2. L.C.M

The Least Common Multiple of two or more integers is always divisible by all the integers it is derived from.  For example, 20 is a multiple of 5 because 5 × 4 = 20, so 20 is divisible by 5 and 2. Because 10 is the smallest positive integer that is divisible by both 5 and 2, it is the least common multiple of 5 and 4.

LCM cam also be understand by this example:

Multiples of 5 are:

5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70 ...

And the multiples of 6 are:

6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...

Common multiples of 5 and 6 are:

30, 60, 90, 120, ....

Hence, the lowest common multiple is simply the first number in the common multiple list i.e 30.

Calculation

- By Prime Factorizations

The prime factorization theorem says that every positive integer greater than 1 can be written in only one way as a product of prime numbers.

Example: To find the value of LCM (9, 48, and 21).

First, find the factor of each number and express it as a product of prime number powers.

Like 9 = 3²,

48 = 2⁴ * 3

21 = 3 * 7

Then, write all the factors with their highest power like 3², 2⁴, and 7. And multiply them to get their LCM.

Hence, LCM (9, 21, and 48) is 3² * 2⁴ * 7 = 1008.

- By Division Method

Here, divide all the integers by a common number until no two numbers are further divisible. Then multiply the common divisor and the remaining number to get the LCM.

2 | 72, 240, 196

  2 | 36, 120, 98

   2 | 18, 60, 49

  3 | 9, 30, 49

     | 3, 10, 49

L.C.M. of the given numbers

= product of divisors and the remaining numbers

= 2×2×2×3×3×10×49

= 72×10×49 = 35280.

Relation between L.C.M. and H.C.F. of two natural numbers

The product of L.C.M. and H.C.F. of two natural numbers = the product of the numbers.

For Example:

LCM (8, 28) = 56 & HCF (8, 28) = 4

Now, 8 * 28 = 224 and also, 56 * 4 = 224

HCF & LCM of fractions:

Formulae for finding the HCF & LCM of a fractional number.

HCF of fraction = HCF of numerator / LCM of denominator

LCM of Fraction = LCM of Numerator / HCF of Denominator

Aptitude Short Tricks to Solve Ratio & Proportion Problems

Heartfully Presented By

AIMS DARE TO SUCCESS

MADE IN INDIA

⏬Telegram Channel ⬇

https://t.me/AIMSDARETOSUCCESS

💡YouTube Channel 🔗

AIMS DARE TO SUCCESS

https://www.youtube.com/channel/UCm-y_cHY75scDiG67Df62dw?sub_confirmation=1

⌛ Web Sites ⏰

👀 For All Competitive Exams Study Material 👀

https://www.aimsdaretosuccess.blogspot.com

👇 For Mathematics Study Material 👇

https://www.aimsdts.blogspot.com

🔦 For Any Queries 🔭

aimsdaretosuccess@gmail.com

If u want to get FREE Study Material Please Add My number 9440345996 in Your All Groups

Joy of sharing is Caring & Helping

Short Tricks to Solve Ratio & Proportion Problems

To make the chapter easy for you all, we are providing you all some Important Short Tricks to solve Ratio & Proportion Questions which will surely make the chapter easy for you all.

Ratio and Proportion

The number of times one quantity contains another quantity of the same kind is called the ratio of the two quantities.

Observe carefully that the two quantities must be of the same kind. There can be a ratio between Rs.20 and Rs 30, but there can be no ratio between Rs 20 and 30 mangoes.

The ratio 2 to 3 is written as 2 : 3 or 2/3.  2 and 3 are called the terms of the ratio. 2 is the first term and 3 is the second term.

Consequent

In the ratio 2 :3 , 2 is the antecedent and 3 is the consequent.

Note:

(1) The word ‘consequent ’ literally means ‘that which goes after’.

(2) since the quotient obtained on dividing one concrete quantity by another of the same kind is an abstract number, the ratio between two concrete quantities of the same kind is an abstract number. Thus, the ratio between Rs 5 and 7 is 5:7.

Compound Ratio

Ratios are compound by multiplying together the antecedents for a new antecedent, and the consequents for a new consequent.

Ex: find the ratio compound of the ratio:

4:3, 9: 13, 26 : 5 and 2:15

Solution;

The required ratio = 

Inverse Ratio

•  If 2:3 be the given ratio, then 1/2: 1/3  or 3 :2 is called its inverse orreciprocal ratio.
• If the antecedent = the consequent, the ratio is called the ratio of equality, such as 3:3.
• If the antecedent >the consequent, the ratio is called the ratio of greater inequality, as 4 :3
• If the antecedent < the consequent, the ratio is called the ratio of less inequality, as 3 : 4.

Ex. Divide 1458 into two parts such that one may be to the other as 2: 7.

Solution:

Proportion

Consider the two ratios:

1^st ratio                      2^nd ratio

6 : 18                           8 : 24

Since 6 is one-third of 18, and 8 is one –third of 24, the two ratios are equal. The equality of ratio is called proportion.

The number 6, 18, 8 and 24 are said to be in proportion.

The proportion may be written as

6 : 18 :: 8 : 24 (6 is to 18 as 8 is to 24)

Or, 6 :18 = 8:24 or 6/18 = 8/24

The numbers 6, 18, 8 and 24 are called the terms. 6 is the first terms, 18 the second, 8 the third, and 24 the fourth. The first and fourth terms, i.e. 6 and 24 are called the extremes (end terms), and the second and the third terms, i.e., 18 and 8 are called the means (middle terms). 24 is called the fourth proportional.

1. If your quantities be in proportion, the product of the extremes is equal to the product of the means.

Let the four quantities 3, 4, 9 and 12 be in proportion.

We have,

2. Three quantities of the same kind are said to be in continued proportion when the ratio of the first to the second is equal to the ratio of the second the third.

The second quantity is called the mean proportional between the first and the third ; and the third quantity is called the third proportional to the first and second.

Thus, 9, 6 and 4 are in continued proportion for 9 :6 ::6 :4.

Hence, 6 is the mean proportional between 9 and 4, and 4 is the third proportional to 9 and 6.

Ex1. Find the fourth proportional to the numbers 6, 8 and 15.

Solution:

If x be the fourth proportional, then 6 : 8 = 15:x

Ex2. Find the third proportional to 15 and 20.

Solution:

Here, we have to find a fourth proportional to 15, 20 and 20. If x be the fourth proportional, we have 15 :20 = 20:x

Direct Proportion: consider the following example.

Ex. 1: If 5 ball cost Rs 8, what do 15 balls cost?

Solution:

It will be seen at once that if the number of balls be increased 2, 3, 4,….times, the price will also be increased 2, 3, 4… times.

Therefore, 5 balls is the same fraction of 15 balls that the cost of balls is of the cost of 15 balls.

5 balls : 15 balls :: Rs8 : required cost

the required cost = Rs

15 * 8 / 5

=Rs 24

This, example is an illustration of what is called direct proportion. In this case, the two given quantities are so related to each other that if one of them is multiplied (or divided) by any number, the other is also multiplied (or divided) by the same number.

Inverse Proportion: Consider the following example

Ex. 1: If 15 men can reap a filed in 28 days, in how many days will 10 men reap it?

Solution:

Here, it will be seen that if the number of men be increased 2, 3,4,….times, the number of days will be decreased 2, 3, 4…times. Therefore, the inverse ratio of the number of men is equal to the ratio of the corresponding number 

The above example is an illustration of what is called inverse proportion. In this case, the two quantities are so related that if one of them is multiplied by any number, the other is divided by the same number, and vice versa.

Ex 2: The employer decreases the number of his employees in the ratio 10 :9 and increase their ways in the ratio 11:12. What is the ratio of his two expenditures?

 Solution:

The required ratio = 10×11 : 9 ×12 = 55 : 54

Ex3: A vessel contains liquid A and B in ratio 5 :3. If 16 liters of the mixture are removed and the same quantity of liquid B is added, the ratio becomes 3 :5. What quantity does the vessel hold?

Solution:

Quicker Method:

When the ratio is reversed (i.e., 5:3 becomes 3 :5), we can use the formula;

Total quantity =

×Quantity  of A in the removed mixture

=

liters.

Aptitude Important Formulas and Shortcuts to solve Percentage

Important Formulas and Shortcuts to solve Percentage

Percentage(%)

Percentage is per‑cent which means parts per hundred(1/100).

 If we have to convert percentage into fraction then it is divide by 100.

Example 1:‑ If we write 45% then its equal to 45/100 or in fraction 9/20or in decimal 0.45

If we have to convert fraction into percentage we have to multiple with 100.

Example 2:‑ if we write 3/5 in fraction it is equal to 60% =3/5x100=60.

Convert Percentage into Decimal:

• 20% = 20/100 = 0.5

Convert Decimal Into Percentage:

• 0.25 = (0.25 × 100) % = 25%
• 1.50 = (1.50 × 100) % = 150%

 Majorly used values shown in Percent, Decimal and Fraction

This table will help you solve questions very fast and easily.Try to remember these fractions because it will save lot of time in your examination.

Types of Formulas and Short Tricks 

Type 1: Percentage Increase/Decrease:

If the price of a commodity increases by R%, then the reduction in consumption so as not to increase the expenditure is: [R/ (100 + R)] x 100%

If the price of a commodity decreases by R%, then the increase in consumption so as not to decrease the expenditure is: [R/ (100 - R)] x 100%

Type 2: Results on Population:

Let the population of a town be P now and suppose it increases at the rate of R% per annum, then:

1.Population after n years = P(1 + R/100)ⁿ

2.Population n years ago =P/(1 + R/100)ⁿ

 Type 3: Results on Depreciation:

Let the present value of a machine be P. Suppose it depreciates at the rate of R% per annum. Then:

1.Value of the machine after n years = P(1 - R/100)ⁿ

2.Value of the machine n years ago = P/[(1 - R/100)]ⁿ

3.If A is R% more than B, then B is less than A by= [R/ (100 + R)] x 100%

4.If A is R% less than B, then B is more than A by= [R/ (100 - R)] x 100%

Note: For two successive changes of x% and y%, net change = {x + y +xy/100}%

Aptitude Important Formulas and Shortcuts to solve Profit and Loss

Important Formulas and Shortcuts to solve Profit and Loss

Cost Price 

Cost Price is the price at which an article is purchased, abbreviated as C.P.

Selling Price

Selling Price is the price at which an article is sold, abbreviated as S.P.

Profit

If the Selling Price exceeds the Cost Price, then there is Profit.

Profit or gain = SP – CP

Profit % = Profit/(C P)×100

S P = (100+gain % )/100  ×C P

C P = 100/(100+gain %)×S P

Loss

If the overall Cost Price exceeds the selling price of the buyer then he is said to have incurred loss.

Loss = C P – S P

Loss % = LOSS/(C P)×100

S P = (100-loss %)/100×C P

C P = 100/(100-loss %)×S P

Profit and Loss Based on Cost Price

To find the percent gain or loss, divide the amount gained or lost by the cost price and multiply it by 100. 

Example: A toy that cost 80 rupees is sold at a profit of 20 rupees. Find the percent or rate of profit.

Answer:

Gain/cost × 100 = % profit.

20/80 × 100 = 25%. - Answer

To find the loss and the selling price when the cost and the percent loss are given, multiply the cost by the percent and subtract the product from the cost.

Example: A damaged chair that cost Rs.110 was sold at a loss of 10%. Find the loss and the selling price.

Answer:

Cost x percent loss = loss.

110 x 1/10 = 11, loss.

Cost - loss = selling price.

110 - 11 = 99, selling price.

Profit and Loss Based on Selling Price

To find the profit and the cost when the selling price and the percent profit are given, multiply the selling price by the percent profit and subtract the result from the selling price.

Example: A toy is sold for Rs. 6.00 at a profit of 25% of the selling price. Separate this selling price into cost and profit.

Answer :

Selling price x % profit = profit.

Selling price = profit + cost.

6.00 x .25 = 1.50, profit.

6.00 - 1.50 = 4.50, cost.

To find the loss and the cost when the selling price and the percent loss are given, multiply the selling price by the percent loss and subtract the result from the selling price.

Example: At a sale, neckties selling at Rs. 50.00 are sold at a loss of 60% of selling price. What is the loss and the original cost?

Selling price x % loss = loss.

Selling price + loss = cost.

50.00 x .60 = 30.00, loss.

50.00 - 30.00 = 20.00, cost.

To find the selling price when the cost and the percent loss are given, add the percent loss to 100% and divide the cost by this sum.

Example: Socks that cost 7.00 per pair were sold at a loss of 25% of selling price. What was the selling price?

Answer: Cost / (100% + % loss) = selling price.

7.00 / 1.25 = 5.60, selling price.

To find the selling price when the profit and the percent profit are given, or to find the selling price when the loss and the percent loss are given, divide the profit or loss by the percent profit or loss.

Note: This rule should be compared with the one under Profit and Loss Based on Cost. The two rules are exactly similar except that in one case 100% represents cost while in the other case 100% represents selling price.

Example: A kind of tape is selling at a profit of 12% of selling price, equal to 18 per yard. What is the selling price of the tape?

Answer: Profit / % profit = selling price.

18 /.12 = 1.50 selling price.

To find the percent profit or loss, divide the amount gained or lost by the selling price.

Example: A candy bar sells for 1.30 at a profit of 65. What percent of profit on selling price does this represent?

Answer: Gain / selling price = % profit.

65 / 1.30 = .5 or 50% profit.

Mark-up Price

Generally the SP is less than the marked price (MP) the difference MP – SP is known as discount, D.

Discount = M P – S P

Discount %, D% = (Discount) / (M P) ×100

To reduce percent loss on cost to percent loss on selling price, divide percent loss on cost by 100% minus percent loss on cost.

 Example: 20% loss on cost is what percent loss on selling price?

Answer:

% loss on cost / (100% - % loss on cost) = % loss on selling price.

0.20 / 80 = .0025 or 25% loss on selling price

To reduce percent loss on selling price to percent loss on cost, divide percent loss on selling price by 100% plus percent loss on selling price.

Example: 20% loss on selling price is what percent loss on cost?

Answer:

% loss on selling price / (100% + % loss on selling price) = % loss on cost.

.20 / 1.20 = .16666 or .16.67% loss on cost.

To reduce percent mark-up (percent profit on cost) to percent profit on selling price, divide percent mark-up by 100% plus percent mark-up.

Example: A coat marked up 60% carries what percent of profit on selling price?

Answer : % profit on cost / ( 100% + % profit on cost ) = % profit on selling price.

.60 / 1.60 = .375 or 37.5% on selling price.

Here we are providing you all the types of questions that have been asked in SSC Exams and How to solve it in an Easy way with  Grade Stack methods:-

Type 1: 

The cost price of 40 articles is the same as the selling price of 25 articles. Find the gain per cent. (CGL-2012)

(a) 65%                                

(b) 60%

(c) 15%                             

(d) 75%

Answer: (b) Gain per cent

=(40-25)/25×100

=15/25×100=60%

Grade Stack methods

In Above question We take x = 40 , y = 25

Then Gain % = (x –y) x 100/ y

Type2: 

Bananas are bought at the rate of 6 for Rs. 5 and sold at the rate of 5 for Rs. 6. Profit per cent is:  (CGL-2004)

(a) 36%                                

(b) 42%

(c) 44%                                

(d) 48%

Answer : (c) To avoid fraction, let the number of bananas bought

LCM of 5 and 6 = 30

CP of 30 bananas

= 5 x 5 = Rs. 25

SP of 30 Bananas = 6 x 6

= Rs. 36

Profit = Rs. (36-25) = Rs. 11

Profit %

= 11/25×100=44%

Grade Stack Method

[(6 x 6 -5x 5)/ (5 x 5)] x 100 = 44%

Type 3:

A man bought oranges at the rate of 8 for Rs 34 and sold them at the rate of 12 for Rs. 27. How many oranges should be sold to earn a net profit of Rs 45? (CGL-2011)

(a) 90                                    

(b) 100

(c) 135                                  

(d) 150

Answers: (a) Let the man buy 24 (LCM of 8 and 12) oranges.

C.P. of 24 oranges  = 34/8  ×24 = Rs. 102

S.P. of 24 oranges = 27/12×24=  Rs. 114

Gain = 114 – 102 = Rs. 12

Rs. 12 = 24 oranges

Rs. 45 =  24/12×45= 90 oranges

Type 4: 

A shopkeeper earns a profit of 12% on selling a book at 10% discount on printed price. The ratio of the cost price to printed price of the book is ?(CGL-2013)

(a) 45 : 56                                

 (b) 50 : 61

(c) 90 : 97                                 

(d) 99 : 125

Answer:  (a) C.P. of the book = Rs. x

Printed price = Rs. y

(y×90)/100=x × 112/100

x/y=90/112=45/56

Type 5: 

A dealer sold two types of goods for Rs 10,000 each. On one of them, he lost 20% and on the other he gained 20%. His gain or loss per cent in the entire transaction was (CGL-2012)

(a) 2% loss                          

(b) 2% gain

(c) 4% gain                         

(d) 4% loss

Answers:  (d) Here, S.P. is same, Hence there is always a loss. Loss per cent =(20×20)/100=4%

 Gradestack Trick

Loss % = (n^2)/100= (20)^2/100= 4%

Where n= 20

Type 6: 

On selling an article for Rs170, a shopkeeper loses 15%. In order to gain 20%, he must sell that article at rupees: (CGL-2013)

(a) 215.50                           

(b) 212.50

(c) 240                                

(d) 210

Answer ; (c) C.P. of article = (200×120)/100 = Rs. 240

Type 7:

An article is sold at a loss of 10%. Had it been sold for Rs. 9 more, there would have been a gain of 12 1/2% on it. The cost price of the article is(CGL – 2002)

(a) Rs. 40                                             

(b) Rs. 45

(c) Rs. 50                                             

(d) Rs. 35

Answers: (a) Let the cost price of the article = Rs. x

S.P. at 10% loss

= x×90/100= Rs. 9x/10

1. P. at 12 1/2 % gain

x  × (100+12 1/2)/100 = Rs. 225x/200

According to the question

9x/10 + 9 = 225x/200

180x + 1800 = 225x

x = Rs. 40

Type 8: 

A sells a suitcase to B at 10% profit. B sells it to C at 30% profit. If C pays Rs 2860 for it, then the price at which a bought it is (CGL-2013)

(a) 1000                                               

(b) 1600

(c) 2000                                               

(d)  2500

Answer:  (c) If the C.P. of the suitcase for A be Rs. x, then

x ×110/100×130/100=2860

x=(2860×100×100)/(110×130) = Rs. 2000

Type 9: 

Arun marks up the computer he is selling by 20% profit and sells them at a discount of 15%. Arun’s net gain percent is 

(CGL-2013)

(a) 4                                      

(b) 2

(c) 3.5                                   

(d) 2.5

Answer (b)

Gradestack method:

r1 = 20 , r2 = 15

Formula = r1 – r2 – (r1 x r2)/100

(20-15-(20×15)/100)

= 20 -18 = 2%

Type10:

A tradesman sold an article at a loss of 20%. If the selling price had been increased by Rs. 100, there would have been a gain of 5%. The cost price of the article was: (CGL-2004)

(a) Rs. 200                                          

(b) Rs. 25

(c) Rs. 400                                          

(d) Rs. 250

Answer  (c) Let the C.P. of article be Rs. x.

105% of x - 80% of x = Rx. 100

25% of x = Rx. 100

x = Rs. (100×100)/25

= Rs. 400

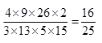
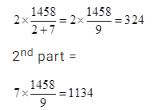
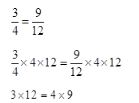
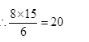
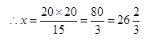
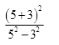
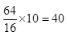
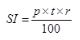
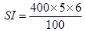
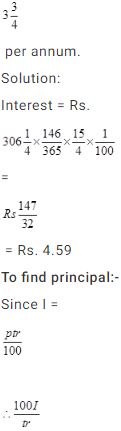
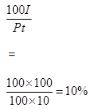
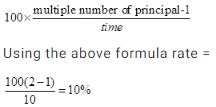
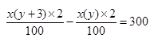
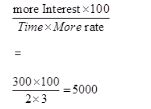
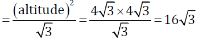
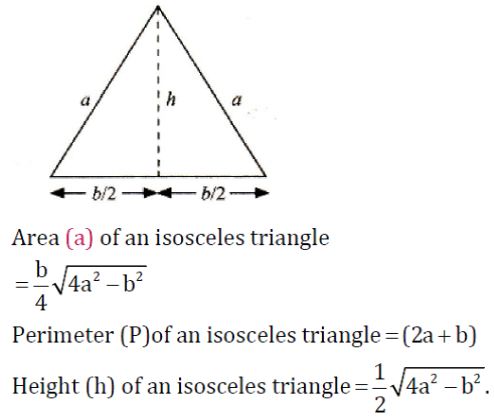
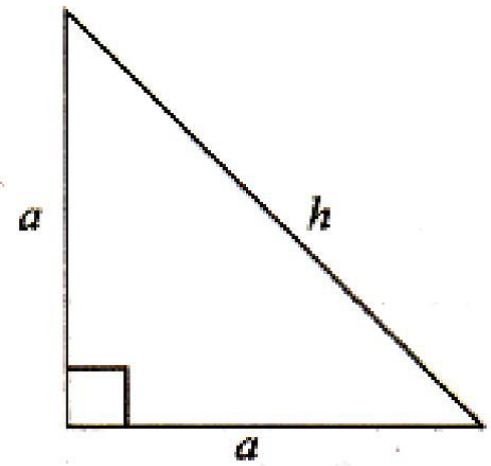
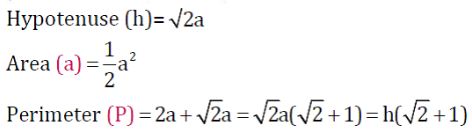
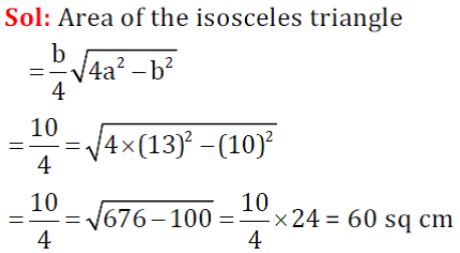
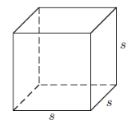
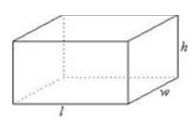
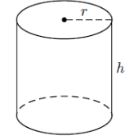
Aptitude Important Concepts & Short Tricks on Speed, Distance & Time

Heartfully Presented By

AIMS DARE TO SUCCESS

MADE IN INDIA

⏬Telegram Channel ⬇

https://t.me/AIMSDARETOSUCCESS

💡YouTube Channel 🔗

AIMS DARE TO SUCCESS

https://www.youtube.com/channel/UCm-y_cHY75scDiG67Df62dw?sub_confirmation=1

⌛ Web Sites ⏰

👀 For All Competitive Exams Study Material 👀

https://www.aimsdaretosuccess.blogspot.com

👇 For Mathematics Study Material 👇

https://www.aimsdts.blogspot.com

🔦 For Any Queries 🔭

aimsdaretosuccess@gmail.com

If u want to get FREE Study Material Please Add My number 9440345996 in Your All Groups

Joy of sharing is Caring & Helping

Important Concepts & Short Tricks on Speed, Distance & Time

Important formulae and facts of Time and Distance

Speed is a very basic concept in motion which is all about how fast or slow any object moves. We define speed as distance divided by time.

Distance is directly proportional to Velocity when time is constant.

• Speed Distance Time formula mathematically written as:- Speed = distance/time

Formula of Time :-time = distance/ Speed

So Formula of time is, time is equal to distance upon speed.

• Formula of Distance:-Distance = (Speed * Time)

Distance = Rate x Time

• To find rate, divide through on both sides by time:

Rate = Distance/Time

• Rate is distance (given in units such as miles, feet, kilometers, meters, etc.) divided by time (hours, minutes, seconds, etc.). Rate can always be written as a fraction that has distance units in the numerator and time units in the denominator, e.g., 25 miles/1 hour.

So distance is simply speed into time.

Note: All three formulae that formula of speed, formula of time and formula of distance are interrelated.

• Convert from kph (km/h) to mps(m/sec)
  For converting kph(kilometre per hour) to mps(meter per second) we use following formula

x km/hr=(x∗5/18) m/sec

• Convert from mps(m/sec) to kph(km/h)
  For converting mps(meter per second) to kph(kilometre per hour)we use following formula

x m/sec= X *(18/5)  km/h

• If the ratio of the speeds of A and B is a : b, then the ratio of the times taken by then to cover the same distance is :1/a : 1/b  or  b : a 
• Suppose a man covers a certain distance at x km/hr and an equal distance at y km/hr. Then,
  the average speed during the whole journey is :- 2xy/(x + y) 

• Relation between time, distance and speed: Speed is distance covered by a moving object in unit time: Speed= Distance covered/ Time Taken

Rule : 1: Ratio of the varying components when other is constant: Consider 2 objects A and B having speed  Sa, Sb.

Let the distance travelled by them are Da and Db respectively and time taken to cover these distances be Ta and Tb respectively.
Let's see the relation between time, distance and speed when one of them is kept constant

• 1. When speed is constant distance covered by the object is directly proportional to the time taken.
     ie; If Sa=Sb then   Da/Db = Ta/Tb
  2. When time is constant speed is directly proportional to the distance travelled. ie; If Ta=Tb then Sa/Sb=Da/Db
  3. When distance is constant speed is inversely proportional to the time taken ie if speed increases then time taken to cover the distance decreases. ie; If Da=Db then  Sa/Sb= Tb/Ta

Rule 2: We know that when distance travelled is constant, speed of the object is inversely proportional to time taken

1. If the speeds given are in Harmonic progression or HP then the corresponding time taken will be in Arithmetic progression or AP
2. If the speeds given are in AP then the corresponding time taken is in HP

Distance Constant

• If distance travelled for each part of the journey, ie d1=d2=d3=...=dn=d, then average speed of the object is Harmonic Mean of speeds.
  Let each distance be covered with speeds s1,s2,...sn in t1,t2,...tn times respectively.
  Then t1 =d/s1
  t2 = d/s2
  tn =d/sn

then, Average Speed=   [(d + d + d+ ... ntimes)]/ [d/s1 + d/s2+ d/s3+ ... d/sn

Average Speed= (n)/[(1/s1  + 1/s2+ .... 1/sn)]

Time Constant

• If time taken to travel each part of the journey, ie t1=t2=t3=…tn=t, then average speed of the object is Arithmetic

Let distance of parts of the journey be d1,d2,d3,...dn and let them be covered with speed s1,s2,s3,...sn respectively.

Then d1=s1 t ,  d2=s2t, d3=s3t, ... dn=snt

then ,  Average Speed= [(s1/t+ s2/t+ .... sn/t)/(t + t+ ...  ntimes)]

Average Speed=( s1+ s2+s3+ ... + sn)/n

Relative Speed

• If two objects are moving in same direction with speeds a and bthen their relative speed is |a-b|
• If two objects are moving is opposite direction with speeds a and bthen their relative speed is (a+b)

Some Question on Above formulas 

Ques  1:- A man covers a distance of 600m in 2min 30sec. What will be the speed in km/hr?

Sol:: Speed =Distance / Time

=Distance covered = 600m, Time taken = 2min 30sec = 150sec

Therefore, Speed= 600 / 150 = 4 m/sec

= 4m/sec = (4*18/5) km/hr = 14.4 km/ hr.

Ques 2:- A car travels along four sides of a square at speeds of 200, 400, 600 and 800 km/hr. Find average speed.?

Sol: Let x km be the side of square and y km/hr be average speed

Using basic formula, Time = Total Distance / Average Speed

x/200 + x/400 + x/600 + x/800= 4x/y

=25x/ 2400 = 4x/ y

= y= 384

Average speed = 384 km/hr

Ques 3: A motor car does a journey in 10 hrs, the first half at 21 kmph and the second half at 24kmph. Find the distance?

Sol:

Distance = (2 x 10 x 21 x 24) / (21+24)

= 10080 / 45

= 224 km.

Ques 4:A boy goes to school at a speed of 3 kmph and returns to the village at a speed of 2 kmph. If he takes 5 hrs in all, what is the distance between the village and the school?

Sol : Let the required distance be x km.

Then time taken during the first journey = x/3 hr.

and time taken during the second journey = x/2 hr.

x/3 + x/2 = 5 => (2x + 3x) / 6 = 5

=> 5x = 30.

=> x = 6

Required distance = 6 km.

Ques 5: Walking ¾ of his speed, a person is 10 min late to his office. Find his usual time to cover the distance?

Sol : Usual time = Late time / {1/ (3/4) - 1)

= 10 / (4/3 -1 )

= 10 / (1/3)

= 30 minutes.

We hope that the post would have cleared all your doubts related to the topic.

Aptitude Short Tricks for Boat and Stream in Quant Section

Short Tricks for Boat and Stream in Quant Section

Upstream: When the boat moves against the current of the river (i.e. in opposite direction), then the relative speed of the boat is the difference of the speed of the boat and stream. It is known as upstream speed.

Remember it with UP as going up the hill means against the direction of the force (speed) of the river.

If speed of boat or swimmer is x km/h and the speed of stream is y km/h then,

• Speed of boat upstream = (x − y) km/h

Downstream: When the boat moves with the current of the river (i.e. in same direction), then the relative speed of the boat is the sum of the speed of the boat and stream. It is known as downstream speed.

Remember it with DOWN as going down the hill means towards the direction of the force (speed) of the river.

If speed of boat or swimmer is x km/h and the speed of stream is y km/h then,

• Speed of boat downstream = (x + y) km/h

Important Points

• When speed of boat is given then it means speed in the still water, unless it is stated otherwise.

Some Basic Formulas 

• Speed of boat in still water is
  = ½ (Downstream Speed + Upstream Speed)

• Speed of stream is
  = ½ (Downstream Speed – Upstream Speed)

Types of Questions asked in Previous Exam By SSC 

Type 1: When the distance covered by boat in downstream is same as the distance covered by boat upstream. The speed of boat in still water is x and speed of stream is y then ratio of time taken in going upstream and downstream is,

Short Trick:

Time taken in upstream : Time taken in Downstream = (x+y)/(x-y)

Example:  

A man can row 9km/h in still water. It takes him twice as long as to row up as to row down. Find the rate of the stream of the river.

Solution:

Time taken in upstream : Time taken in Downstream = 2 : 1

Downstream speed : Upstream speed = 2 : 1

Let the speed of man = B, & speed of stream = S

B + S : B – S = 2/1

By using Componendo & Dividendo

B/R = 3/1, R = B/3

R = 9/3 = 3km/h
Type 2: A boat cover certain distance downstream in t₁ hours and returns the same distance upstream in t₂ hours. If the speed of stream is y km/h, then the speed of the boat in still water is:

Short Trick:

Speed of Boat = y [(t₂ + t₁) / (t₂ – t₁)]

Example

A man can row certain distance downstream in 2 hours and returns the same distance upstream in 6 hours. If the speed of stream is 1.5 km/h, then the speed of man in still water is

Solution:

By using above formulae

= 1.5 [(6+2) / (6-2)] = 1.5 * (8/4) = 1.5 * 2 = 3km/h

Type 3: A boat’s speed in still water at x km/h. In a stream flowing at y km/h, if it takes it t hours to row to a place and come back, then the distance between two places is

Short Trick:   Distance = [t*(x² – y²)]/2x

Example

A motor boat can move with the speed 7 km/h. If the river is flowing at 3 km/h, it takes him 14 hours for a round trip. Find the distance between two places?

Solution: By using above formulae

= [14 * (7² – 3²)]/2* 7 = [14 * (49-9)]/2*7

= 14*40/2*7 = 40km

Type 4:  A boat’s speed in still water at x km/h. In a stream flowing at y km/h, if it takes t hours more in upstream than to go downstream for the same distance, then the distance is

Short Trick: Distance = [t*(x² – y²)]/2y

Example

A professional swimmer challenged himself to cross a small river and back. His speed in swimming pool is 3km/h. He calculated the speed of the river that day was 1km/h. If it took him 15 mins more to cover the distance upstream than downstream, then find the width of the river?

Solution: By using the above formulae

Distance = [t*(x² – y²)]/2y

= [(15/60) (3² – 1²)]/2*1

= [(1/4) * 8] / 2

= 2/2 = 1 km.

Type 5: A boat’s speed in still water at x km/h. In a stream flowing at y km/h, if it cover the same distance up and down the stream, then its average speed is

Short Trick: Average speed = upstream * downstream / man’s speed in still water

Note: The average speed is independent of the distance between the places.

Example

Find the average speed of a boat in a round trip between two places 18 km apart. If the speed of the boat in still water is 9km/h and the speed of the river is 3km/h?

Solution: Average speed = upstream * downstream / man’s speed in still water

Average speed = 6 * 12 / 9 = 8km/h

Aptitude Important Short Tricks to solve Simple Interest Questions

Important Short Tricks to solve Simple Interest Questions

To make the chapter easy for you all, we are providing you all some Important Short Tricks to solve Simple Interest Questions which will surely make the chapter easy for you all.

Important Short Tricks to solve Simple Interest Questions

Interest is the money paid by the borrow to the lender for the use of money lent.
The sum lent is called the Principal. Interest is usually calculated at the rate of so many rupees for every Rs.100 of the money lent for a year. This is called the rate per cent per annum.
‘Per annum’ means for a year. The words ‘per annum’ are sometimes omitted. Thus, 6 p.c. means that Rs.6 is the interest on Rs.100 in one year.
The sum of the principal and interest is called the amount. The interest is usually paid yearly, half-yearly or quarterly as agreed upon.
Interest is of two kind, Simple and Compound. When interest is calculated on the original principal for any length of time it is called simple interest. Compound interest is defined in the next chapter.

To find Simple Interest, multiply the principal by the number of years and by the rate per cent and divide the result by 100.

This may be remembered in the symbolic form

Where I = Interest, p = principle, t = number of years, r = % rate

Ex. 1. Find the simple interest on Rs.400 for 5 years at 6 percent.

Solution:

Interest for a number of days

When the time is given in days or in years and days, 365 days are reckoned to a year. But when the time is given in months and days, 12 months are reckoned to a year and 30 days to the month. The day on which the money is paid back should be include be but not the day on which it is borrowed, ie, in counting, the first day is omitted.

Ex. 2. Find the simple interest on Rs.306. 25 from March 3^rd to July 27^that

Ex.3. What sum of money will produce Rs.143 interest in

Ex. 4. A sum of Rs.468.75 was lent out at simple interest and at the end of 1 year 8 months the total amount was Rs500. Find the rate of interest per cent annum.

Solution:

Here, P =Rs468.75, t =

Ex. 5. In what time will Rs.8500 amount to Rs.15767.50 at

Miscellaneous Examples on Simple Interest:-

Ex.6: The simple interest on a sum of money is 1/9^th of the principal, and the number of years is equal to the rate per cent per annum. Find the rate per cent.

Solution:

Let principal = P, time = t year, rate = t

Then,

Ex. 7: The rate of interest for the first 2 yrs is 3% per annum, for the next 3 years is 8% per annum and for the period beyond 5 years 10% per annum.To fetch an interest of 1520 in six years, money did he deposit?

Solution

Let his deposit be = Rs 100

Interest for first 2 yrs = Rs 6

Interest for next 3 yrs = Rs 24

Interest for the last year = Rs 10

Total interest = Rs 40

When interest is Rs 40, deposited amount is Rs 100

when interest is Rs 1520, deposited amount =

 Ex.8: A sum of money doubles itself in 10 years at simple interest. What is the rate of interest?

Solution:

Let the sum be Rs 100

After 10 years it becomes Rs 200

Interest = 200 - 100 = 100

Direct formula:

Time × Rate = 100 (Multiple number of principal – 1)

Ex.9: A sum was put at a certain rate for 2 yrs. Had it been put at 3% higher rate, it would have fetched Rs 300 more. Find the sum.

Solution:

Let the sum be Rs x and the original rate be y% per annum. Then, new rate = (y+3) % per annum

xy +3x – xy =15,000 or, x =5000

Thus, the sum =Rs 5000

Gradestack Method : Direct Formula

Sum = 

Ex.10. The simple interest on a certain sum of money at 4% per annum for 4 yrs is Rs 80 more than the interest on the same sum for 3 yrs at 5% per annum. Find the sum.

Solution:

Let the sum be Rs.x , then, at 4% rate for 4 yrs the simple interest =

We hope you all like the post. Don’t forget to share your feedback with us in the comment box.

To view the Important Short Tricks to solve Compound Interest Questions, click on the link given below:

Aptitude Shortcut and Formulas of Mensuration (Triangle)

Shortcut and Formulas of Mensuration (Triangle)

Today we are covering Shortcuts and formulas for how to solve Triangle problem in Mensuration. Before moving ahead with formulas of Triangle, let us first understand basics of Mensuration.

MENSURATION-I (Area & Perimeter)

AREA

The area of any figure is the amount of surface enclosed within its bounding lines. Area is always expressed in square units.

UNITS OF MEASURING AREA

• 100 sq Millimeters = 1sq centimeter
• 100 sq centimeter = 1sq decimeter
• 100 sq decimeters = 1sq meter
• 100 sq meters = 1sq decameter or arc
• 10,000 sq meters =1 hectare
• 1,000,000 sq meters = 100 hectares = 1 sq kilometer

Perimeter

The perimeter of a geometrical figure is the total length of the sides enclosing the figure.

Triangles and their formulas

A triangle is a closed figure bounded by three sides. ABC is a triangle.

The sides A         B, BC and AC are respectively denoted by c, a and b.

Area of a triangle (A)

(a) A 1/2 (base x  height)=  (1/2) a x h

(b) 

where formula is known as Hero’s formula. Perimeter (P) = a +b +c =2s.

2. Right Angled Triangle

A triangle having one of its angles equal to 90° is called a right-angled triangle. The side opposite to the right angle is called the hypotenuse.

In a right angled triangle,

(Hypotenuse)² = sum of squares of sides

i.e h^2 = a^2 + b^2

Area (a)= 1/2(product of the sides containing the right angle)

i.e. A = (1/2) ab

3. Equilateral Triangle

A triangle whose all sides are equal is called an equilateral triangle.

Example: Height of an equilateral triangle is 4 3 cm. Find its area.

Sol: Area of equilateral triangle

4. Isosceles Triangle

A triangle whose two sides are equal is an isosceles triangle.

5. Isosceles Right-angled Triangle

An isosceles right-angled triangle has two sides equal with equal sides making 90° to each other.

If the perimeter of an isosceles triangle is P and the base is b, then the length of the equal sides is ( pb/2)

If the perimeter of an isosceles triangle is P and the length of the sides is a, then base is (P−2a).

Example: If the base of an isosceles triangle is 10 cm and the length of equal sides is 13 cm, find its area.

Sol: Area of the isosceles triangle

Here's a short quiz based on the above facts for practicing.

Aptitude Important Mensuration (3D) Formulas

Important Mensuration (3D) Formulas

Cube

• s = side
• Volume: V = s^3
• Lateral surface area = 4a²
• Surface Area: S = 6s^2
• Diagonal (d) = s√3

Cuboid

• Volume of cuboid: length x breadth x width
• Total surface area = 2 ( lb + bh + hl)

Right  Circular  Cylinder

• Volume of Cylinder = π r^2 h
• Lateral Surface Area (LSA or CSA) = 2π r h
• Total Surface Area = TSA = 2 π r (r + h)

Right Circular Cone

• l^2 = r^2 + h^2
• Volume of cone = 1/3 π r^2 h
• Curved surface area: CSA=  π r l
• Total surface area = TSA = πr(r + l )

Frustum of a Cone

• r = top radius, R = base radius,
• h = height, s = slant height
• Volume: V = π/ 3 (r^2 + rR + R^2)h
• Surface Area: S = πs(R + r) + πr^2 + πR^2

Sphere

• r = radius
• Volume: V = 4/3 πr^3
• Surface Area: S = 4π^2

Hemisphere

• Volume-Hemisphere = 2/3 π r^3
• Curved surface area(CSA) = 2 π r^2
• Total surface area = TSA = 3 π r^2

Prism

• Volume = Base area x height

• Lateral Surface area = perimeter of the base x height

Pyramid

• Volume of a right pyramid = (1/3) × area of the base × height.
• Area of the lateral faces of a right pyramid = (1/2) × perimeter of the base x slant height.
• Area of whole surface of a right pyramid = area of the lateral faces + area of the base.

Aptitude Important notes on Triangles and their Properties

Heartfully Presented By

AIMS DARE TO SUCCESS

MADE IN INDIA

⏬Telegram Channel ⬇

https://t.me/AIMSDARETOSUCCESS

💡YouTube Channel 🔗

AIMS DARE TO SUCCESS

https://www.youtube.com/channel/UCm-y_cHY75scDiG67Df62dw?sub_confirmation=1

⌛ Web Sites ⏰

👀 For All Competitive Exams Study Material 👀

https://www.aimsdaretosuccess.blogspot.com

👇 For Mathematics Study Material 👇

https://www.aimsdts.blogspot.com

🔦 For Any Queries 🔭

aimsdaretosuccess@gmail.com

If u want to get FREE Study Material Please Add My number 9440345996 in Your All Groups

Joy of sharing is Caring & Helping

Important notes on Triangles and their Properties

Today we will be covering a very important topic from the Advance Maths part of the Quantitative Aptitude section that is – Important notes on Triangles and their Properties.

Triangles and their properties

Area of triangle

1. When base and corresponding height is known: ½ * base * height = ½*c*h

2. When all sides are given (Heron’s formulae): {s (s - a) (s - b) (s - c)}^1/2  where, s = (a+b+c)/2

3. When two sides and corresponding angle is given.: ½ a*c*sinθ

4. When all the median are given (Median is a line joining the vertex to the opposite side at midpoint): 4/3 * {s(s – m₁) (s – m₂) (s –m₃)}^1/2

Note: Where, s = (m₁+m₂+m₃)/2, m₁,m₂,m₃ are three medians of the Triangle.

5. When all the heights are given: 1/Area of ∆ = 4 {G (G – 1/h₁) (G – 1/h₂) (G – 1/h₃),

Note: Where, G = ½ (1/h₁ + 1/h₂ + 1/h₃)

Sine formulae of triangle

a/SinA = b/sinB = c/SinC = 2R Where, R is Circumradius

Cosine Formulae of triangle

CosA = b² +c² – a² / 2bc

CosB= a² +c² – b² / 2ac

CosC = b² +a² – c² / 2ba

An interesting result based of cosine formulae

If in a triangle CosA = b² +c² – a² / 2bc, Whereas b & c are the smaller sides then

Case I, b² +c²  is greater than a² then angle A is acute.

Case II, b² +c²  is smaller than a² then angle A is obtuse.

Case III, b² +c²  is equals to a² then angle A is Right Angle.

For example,

Ques: Find the type of the triangle ABC whose 3 sides are of length 11, 3 & 9.

Solution: Sum of square of two smaller sides is 3² + 9² = 9 + 81 = 90

Square of largest side is 11² = 121.

Hence, this triangle is obtuse angled triangle.

TRIANGLES AND ITS CERVICES

Medians of a Triangle

The medians of a triangle are line segments joining each vertex to the midpoint of the opposite side. The medians always intersect in a single point, called the centroid.

In the adjoining figure D, E, & F are midpoints of the side of the triangle while Line Segment AD, BE & CF are median. They are meeting at a common point I which is the centroid.

Properties:

1. Centroid divides the Median in the ratio 2:1. i.e AI/ID = 2/1
2. Apollonius Theoram:- To find the length of median when all sides are given: 4 * AD² = 2(AC² + AB²) – BC²

3. All 3 median of a triangle divides the triangle in 6 equal parts.

i.e. ar of ∆AFI = ar of ∆AEI = ar of ∆BFI = ar of ∆BDI= ar of ∆CDI= ar of ∆CEI= ar of ∆ABC/6

Angle Bisectors

Angle bisectors are the line segment which bisects the internal angles of the triangle. All the three angle bisectors meet at a common point called as Incentre.

In the adjoining figure Line Segment A₁T₁, A₂T₂, & A₃T₃ are Angle Bisector. While point I is Incentre of the triangle.

Incentre is the only point from which we can draw a circle inside the triangle which will touch all the sides of the triangle at exactly one point & this circle has a special name known as Incircle. And the radius of this circle is known as Inradius.

Properties:

1. Inradius = Area of ∆ A₁A₂A₃ / Semi perimeter of ∆ A₁A₂A₃
2. Angle formed at the incentre by any two angle bisector: Angle A₁IA₃  = Angle A₁A₂A₃ /2) + 90^o

Perpendicular Bisectors of Sides of the Triangle

When the perpendicular bisectors of the side of the triangle is drawn they meet at a common point known as circumcentre.

This circumcentre is a special point as from this point we can draw a circle which will enclose the triangle in a way that all the vertex of the triangle lie on the circle. The radius of this circle is known as circumradius.

Properties:

In the adjoining figure DP, EP, & FP are perpendicular bisector of sides of the triangle. Point P is circumcentre.

1. Circumradius = length of side AC * CB * BA / 4 * Area of triangle
2. Angle formed at the circumcentre by any two linesegment joining circumcentre to the vertex: Angle APC = 2 * Angle ABC

Altitude of the Triangle

The orthocenter of a triangle is the point where the three altitudes meet. This point may be inside, outside, or on the triangle.

In the adjoining figure AD, BE, & CF are three altitudes of a triangle. And point O is the orthocenter.

Properties:

1. Angle BOC + Angle BAC = 180^o

SIMILAR TRIANGLE

If two triangles are similar, then the corresponding sides we have, shows the following relation:

• The ratio of sides of triangle is proportional to each other.

Like AB/DE = BC/EF = CA/FD

For example:

If AB = 6cm, BC = 10cm & DE = 2cm. Find EF

Solution: AB/DE = BC/EF, 6/2 = 10/EF, Therefore EF = 2*10/6 = 10/3

• The height, angle bisector, inradius & circumradius are proportional to the sides of triangle.

Median ∆ABC / Median ∆DEF = Height ∆ABC/ Height ∆DEF = AB/DE

• The areas of the triangles are proportional to the square of the sides of the corresponding triangle.

Area ∆ABC/ Area ∆DEF = (AB/DE) ²

For example:

If AB = 6cm, DE = 10cm & Area of ∆ABC is 135 sqcm. Find Area of ∆DEF.

Solution: Area ∆ABC/ Area ∆DEF = (AB/DE) ²

135/ Area ∆DEF = (6/10)² , Area ∆DEF = 135*(5/3)² = 375 sqcm.

In a right angled triangle, the triangles on each sides of the altitude drawn from the vertex of the right angle to the hypotenuse are similar to each other and to the parent triangle.

• ∆ ABC ≈ ∆ ABD
• ∆ ABC ≈ ∆ CBD
• ∆ DBC ≈ ∆ ABD

Proof: In ∆ ABC & ∆ ABD. Angle B and Angle D is 90^o. & Angle A is common in both. Hence by AA rule Both triangles are similar.

Some Important Question are as follows::

(1)In the given figure =?

1. 360°
2. 720°
3. 180°
4. 300°

Ans.  (a)

Here in triangle AEC

1. 900°
2. 720°
3. 180°
4. 540°

Ans.  (c)

In star like figure we calculate the sum of angle by using formula (n-4) 180, when n is the number of point in the star.

(3) In the given figure below, if AD = CD = BC, and 

(a)  32⁰

(b)  84⁰

(c)   64⁰

(d)  can't be determined

Ans.  (c)

Here 

(4)In the trapezium ABCD shown below, AD || BC and AB = 6, BC = 7, CD = 8, AD = 17, if sides AB and CD are extended to meet at E, find the measure of

 

(a) 120⁰

(b)  100⁰

(c)   80⁰

(d)  90⁰

Ans.  (d)

(5)In the given figure, ABCD is a rhombus and AR = AB = BP, then the value of

is

(a)  60⁰

(b)  90⁰

(c)   120⁰

(d)  75⁰

Ans.  (b)