Concepts of Percentages and its Important Shortcuts
1. A+B+AB/100 When A and B both are positive change
2. A-B-AB/100 When A is positive change and B is negative change
3. -A+B-AB/100 When A is negative change and B is positive change.
4. -A-B+AB/100 When A and B both are negative change.
Important: There is no need to remember above formulas, you have to just remember
±A ± B ±AB/100 and put the sign of change, if negative, then (-) and positive then, (+) but keep in mind that sign of AB is product of signs of A and B.
±A ± B ±AB/100 and put the sign of change, if negative, then (-) and positive then, (+) but keep in mind that sign of AB is product of signs of A and B.
Example1: The price of a book is reduced by 10% and sale of the book is increased by 15%. Find the net effect on revenue.
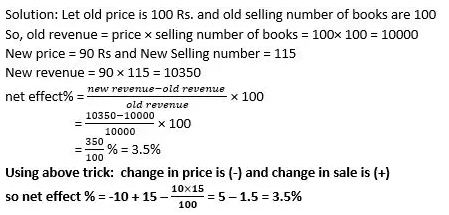
Example2 : If length and breadth of a rectangle is increased by 5% and 8% respectively. Find the % change in area of the rectangle.
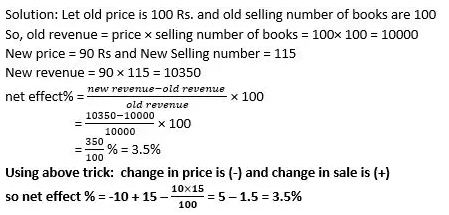
Example2 : If length and breadth of a rectangle is increased by 5% and 8% respectively. Find the % change in area of the rectangle.

Concept 2:
New solution × new % = old solution × old %
This formula is applicable for the commodity which is constant in the solution or mixture, its quantity doesn’t change after mixing in solution.
This formula is applicable for the commodity which is constant in the solution or mixture, its quantity doesn’t change after mixing in solution.
Example3: A mixture of sand and water contains 20% sand by weight. Of it 12 kg of water is evaporated and the mixture now contains 30% sand.
Solution: In this sand is constant in the mixture. So we will apply this formula on sand not on water.
(a)Find the original mixture.
Let the original mixture is P kg, So new mixture = (P-12) kg
old% = 20 and new % = 30
new solution × new % = old solution × old %
(P-12)× 30% = P × 20%
3P – 36 = 2P
P = 36 Kg.
(b) Find the quantity of sand and water in the original mixture.
Quantity of sand in original mixture = 20% of 36 = 7.2 Kg
Quantity of water in original mixture = 80% 0f 36 = 28.8 Kg
OR = Quantity of mixture – quantity of sand = 36 -7.2 = 28.8 Kg
(P-12)× 30% = P × 20%
3P – 36 = 2P
P = 36 Kg.
(b) Find the quantity of sand and water in the original mixture.
Quantity of sand in original mixture = 20% of 36 = 7.2 Kg
Quantity of water in original mixture = 80% 0f 36 = 28.8 Kg
OR = Quantity of mixture – quantity of sand = 36 -7.2 = 28.8 Kg
Example 4: 30 litres of a mixture of alcohol and water contains 20% alcohol. How much litre of water must be added to make the alcohol 15% in the new mixture?
Solution: only water is added in the mixture so, there is no change in alcohol. We will apply above formula on alcohol. Let water added is P litres.
Old mixture = 30 litres, old % of alcohol = 20%
New mixture = 30+P litres, new % of alcohol = 15
using, new solution × new % = old solution × old %
(30+P) × 15% = 30 × 20%
P = 10 litres , hence 10 litres of water is added.
Concept 3

Example 5: If the price of milk increased by 25%, by how much percent must Rahul decrease his consumption, so as his expenditure remains same.
Solution: Let price of milk is 20 Rs/litre and Rahul consumes 1 litre milk.
Expenditure of Rahul = price × consumption
Now price of milk is increased by 25%, so new price is (125/100)× 20 = 25 Rs.
but his expenditure remains same
but his expenditure remains same
So, new consumption × new price = old price × old consumption
new consumption × 25 = 20 × old consumption
new consumption =(20/25) × old consumption
new consumption% = (20/25)× old consumption × 100
new consumption% = 80% of old consumption
decrease in consumption = 20 %
new consumption × 25 = 20 × old consumption
new consumption =(20/25) × old consumption
new consumption% = (20/25)× old consumption × 100
new consumption% = 80% of old consumption
decrease in consumption = 20 %
Using above trick: Given, price % is increased so sign will be (+) and consumption % will decrease.
Decrease in consumption =(25/125) × 100 = 20%
Example 6: If the price of milk decrease by 25%, by how much percent must Rahul increase his consumption, so as his expenditure remains same.
Solution: Let price of milk is 20 Rs/litre and Rahul consumes 1 litre milk.
Expenditure of Rahul = price × consumption
Now price of milk is decreased by 25%, so new price is × 20 = 15 Rs.
but his expenditure remains same
So, new consumption × new price = old price × old consumption
new consumption × 15 = 20 × old consumption
new consumption = (20/15)× old consumption
new consumption% = (20/15)× old consumption × 100
new consumption% = 133(1/3)% of old consumption
increase in consumption = 33(1/3) %
new consumption × 15 = 20 × old consumption
new consumption = (20/15)× old consumption
new consumption% = (20/15)× old consumption × 100
new consumption% = 133(1/3)% of old consumption
increase in consumption = 33(1/3) %
Using above trick: given price % is decreased so sign will be (-) and consumption % will increase.
Increase in consumption = (25/75) x 100 = 33(1/3)%
Increase in consumption = (25/75) x 100 = 33(1/3)%
Concept 4:
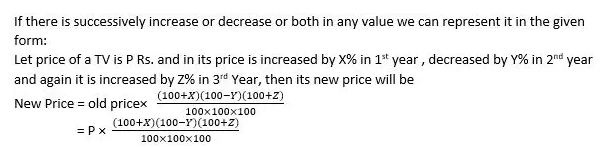
Example 7: The population of a town is 6000. It increases 10% during 1styear, increases 25% during 2nd year and then again decreases by 10% during 3rd year. What is the population after 3 year.
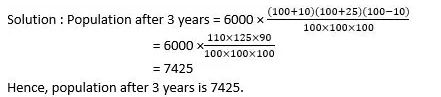
Example 8: The population of a village increases by 10% during the first year, decreased by 12% during 2nd year and again decreased by 15% during 3rd year. If the population at the end of 3rd year is 2057.
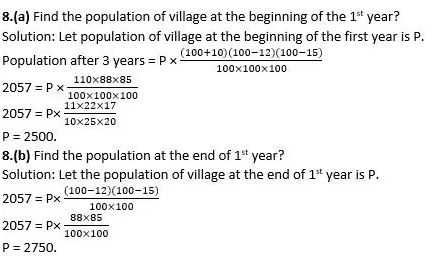
No comments:
Post a Comment