Aptitude Percentage Problems

Percentages: Formulas, Tricks , Shortcuts, and example

In this article, we provide you a short and effective summary for Percentages. We cover a list of 15 formulas and short-cuts that you can use for Percentage questions. The following is a list of important formulas for Percentage:

1. Percent implies “for every hundred”.
% is read as percentage and x % is read as x per cent.

2. To calculate p % of y

(p/100) x y = (p x y)/100

p % of y = y % of p

3. To find what percentage of x is y: y/x × 100

4. To calculate percentage change in value
Percentage change = {change/(initial value)} x 100

5. Percentage point change = Difference of two percentage figures

6. Increase N by S % = N( 1+ S/100 )

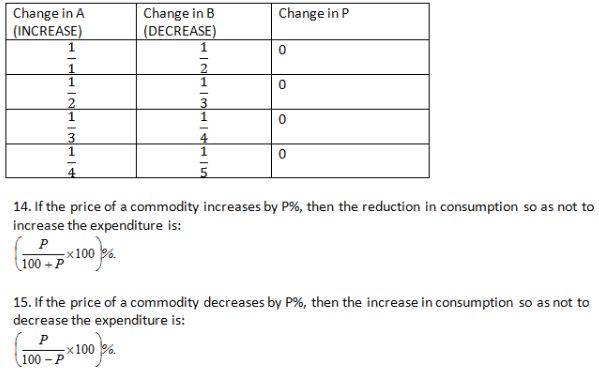
7. Decrease N by S % = N (1 – S/100)

8. If the value of an item goes up/down by x%, the percentage reduction/increment to be now made to bring it back to the original point is 100x/ (100 + x) %.

9. If A is x% more /less than B, then B is 100x/(100 + x) % less/more than A.

10. If the price of an item goes up/down by x %, then the quantity consumed should be reduced by 100x/ (100 + x)% so that the total expenditure remains the same.

11. Successive Percentage Change
If there are successive percentage increases of a % and b%, the effective percentage increase is:
{(a + b + (ab/100)}%

12. Percentage – Ratio Equivalence:

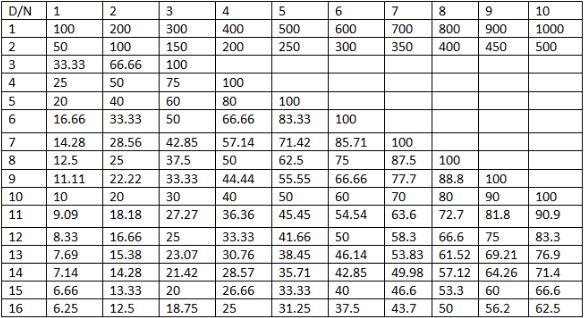
N is Numerator
D is the Denominator

13. Product Stability Ratio:
A × B = P
If A is increased by a certain percentage, then B is required to be decreased by a certain percentage to keep the product P stable.

Expressing the percentage figures in ratios:

 

Problem Type-1:

If a reduction of p % in the price of an article enables a person to buy y kg more for Rs R,then we can arrive at the following results:

Reduced price=> Rp/100y per kg

Original prices per kg= Rp/(100-p)y per kg

Example: A reduction of 21% in the price of an item enables a person to buy 3 kg more for 100. Thereduced price of item per kg is:

(a) Rs. 5.50

(b) Rs. 7.50

(c) Rs. 10.50

(d) Rs. 7.00

Solution:(d)

Reduced price will be:

Rp/100y per kg

In our case R= Rs. 100 , x=21% , y=3kg

{(100 x 21)/(100 x 3)} = Rs. 7

Alternate method:

Expenditure = price per quantity × consumption

E = P × Q =100……. (1)

Now, as per the question,

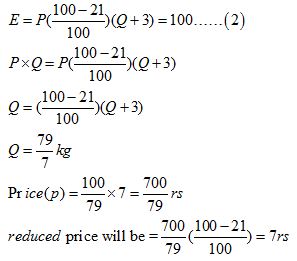
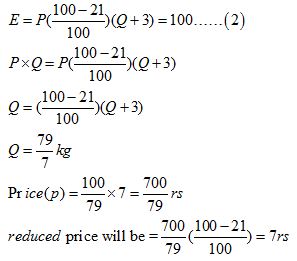
Problem Type-2: Problems based on mixtures

Example: A vessel has 60 L of solution of acid and water having 80% acid. How much water is to be added to make it solution in which acid forms 60%?

(a) 48 L

(b) 20 L

(c) 36 L

(d) None of these

Solution: (b)

Given, percentage of acid = 80%

Then, percentage of water = 20%

In 60L of solution, water = (60 x 20)/ 100 = 12L

Let p liter of water is to be added.

According to the question,

=>{(12 + p)/(60 + p)} x 100 = 40 (∵ 100 – 60 = 40% water)

=>1200 + 100p = 2400 + 40p

⇒ 60p = 1200

p= 20L

Problem Type-3: Problems based on Ratios and Fractions

Example: If the numerator of a fraction is increased by 20% and the denominator is decreased by 5%, the value of the new fraction become 5/2. The original fraction is:

(a) 24/19

(b) 3/18

(c) 95/48

(d) 48/95

Solution: (c)

Let original fraction be p/y

According to the question,

{(120/100)p/(95/100)y} = 5/2

120p/95y = 5/2

=> p/y = (5/2)x (95/120) = 95/48.

Problem Type-4: Problems based on Income, salary, expenditure

Example:The monthly income of a person was Rs 13500 and his monthly expenditure was Rs 9000. Nextyear his income increased by 14% and his expenditure increased by 7%. The per cent increase inhis savings was:

(a) 7%

(b) 21%

(c) 28%

(d) 35%

Solution: (c)

Given, monthly income = 13500 and expenditure = 9000

Then, original savings= Rs. (13500-9000) = Rs 4500

New income = 114% of Rs. 13500 = Rs 15390

New expenditure= 107% of Rs 9000 = Rs 9630

New saving = Rs. (15390 – 9630) = Rs 5760

NS = new savings

OS = Original savings

Percentage increase in savings = {(NS – OS)/OS} X 100

{(5760 – 4500)/4500} X 100 = (1260/4500)X 100 = 28%

Problem Type-5: Problems based on students and marks

Shortcut-1 for the problem type:

A candidate scores x% is an examination fails by ‘a’ marks, while another candidate who scores y% marks and get b marks more than the maximum required passing marks, then the maximum marks for the examination is given by

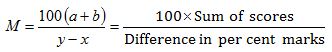
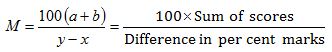
Shortcut-2 for the problem type:

In an examination a% of total number of candidates failed in a subject X and b% of total number of candidates failed in subject Y and c% failed in both subjects, then percentage of candidates, who passed in both the subjects, is [100 – (a + b – c)]%.

Example: In a quarterly examination a student secured 30% marks and failed by 12 marks. In the same examination another student secured 40% marks and got 28 marks more than minimum marks to pass. The maximum marks in the examination is:

(a) 300

(b) 500

(c) 700

(d) 400

Example: In an examination, 52% of the candidates failed in English and 42% failed in Mathematics. If17% failed in both the subjects, then the percentage of candidates who passed in both the subjects, was:

(a) 23%

(b) 21%

(c) 25%

(d) 22%

Solution: (a)

In an examination a% of total number of candidates failed in a subject X and b% of total number of

candidates failed in subject Y and c% failed in both subjects.

Then, percentage of candidates who passed in both the subjects: [100–(a + b– c)%].

Why so?

We need to subtract failed candidate from total to calculate pass candidates, but in this process, we subtract people who were fail in both of subjects twice, so we added c again.

Now equation can be read as [ 100—a-b+c]

Here, a = 52, b = 42 and c = 17, then Percentage of candidates who passed in both the subjects

= [100 –(52 +42–17)]

= 100–77=23%

Problem Type-2: Problems based on percentage in excess or in short

Example: lf A has 4/5 of the number of books that shelf B has. If 25% of the books A are transferred to B and then 25 % of the books from B are transferred to A then the percentage of the total number of books that on shelf A is:

(a) 25%

(b) 50%

(c) 75%

(d) 100%

Solution: (b)

Let the number of books in shelf B be 100.

∴ Number of books in shelf A = {(100 x 4)/5} = 80

On transferring 25% i.e.,of books of shelf A to shelf B, the books on

shelf B = {100 + (80 x 25)/100}

B = 100 + 20 = 120

Books left in shelf A = 80-20 = 60

Again, on transferring 1/4th books of shelf B to shelf A, the books on

shelf A = {60 + (120/4)} = 90

Total no of books in A and B = 120 +60 = 180

Required percentage of books on shelf A = (90/180) x 100 = 50%

Problem Type-3: Problems based on percentages and number system

Example: A number, on subtracting 15 from it, reduces to its 80%. What is 40% of the number?

(a) 75

(b) 60

(c) 30

(d) 90

Solution: (c)

Let the number be p.

According to the question,

p – 15 = p(80/100)

p -15 = 4p/5

⇒ 5p – 75 = 4p ⇒ p = 75

Now, 40% of 75 = (75 x 40)/ 100 = 30